Forum Index - Topic Index Forum Index - Topic Index How to use of Astah (Pro/SysML/GSN/Com) How to use of Astah (Pro/SysML/GSN/Com)
 use of Submachine state ? use of Submachine state ? |
| Threaded | Oldest First | Previous Topic | Next Topic | Bottom |
| Poster | Thread |
|---|---|
| Joba | Posted on: 2009/5/7 8:45 |
Developer   Joined: 2006/6/6 From: Posts: 969 |
Re: use of Submachine state ? - thank u You are welcome, rathinamsm.
 Cheers, Satomi |
| rathinamsm | Posted on: 2009/5/5 16:15 |
Just popping in   Joined: 2009/4/22 From: Posts: 6 |
Re: use of Submachine state ? - thank u Dear satomi san,
Thank u for exlaining to use the Stub Machine state diagram.  regards rathinam.m
|
| Joba | Posted on: 2009/4/30 5:27 |
Developer   Joined: 2006/6/6 From: Posts: 969 |
Re: use of Submachine state ? Hello rathinam,
To represent a Submachine state, drag and drop the target Statemachine diagram from the Structure Tree onto another Statemachine diagram open in the diagram editor. 1. Open a Statemachine diagram (Statemachine diagram B in the figure) in the Diagram Editor 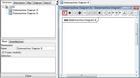 2. Drag & Drop another Statemachine (Statemachine diagram A in the figure) onto the Diagrem Editor. 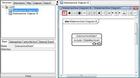 Cheers, Satomi |
| rathinamsm | Posted on: 2009/4/29 18:48 |
Just popping in   Joined: 2009/4/22 From: Posts: 6 |
Re: use of Submachine state ? Hi
I cheked out the 1.5 version. the book is very useful. my doubts gets clarified. But i'm using Jude Community version, In that version, the 1. I have tool to draw the state. and 2. Dont have the state to draw the SubMachine state. regards rathinam.m
|
| Joba | Posted on: 2009/4/28 10:11 |
Developer   Joined: 2006/6/6 From: Posts: 969 |
Re: use of Submachine state ? Hi Rathinam.M,
Please check out the OMG-Unified Modeling Language, v1.5 3.82.3 Example (P. 3-153) It clearly shows you how to use this model with examples.  The specification documentation is available from here. Cheers, Satomi |
| rathinamsm | Posted on: 2009/4/27 16:35 |
Just popping in   Joined: 2009/4/22 From: Posts: 6 |
Re: use of Submachine state ? Hi Joba,
Thank you. Now i got the explanation. I dont know to use the tool, to make a sample I tried with composite state and shallow history. How to use the substate in submachine state tool. "if u have any sample diagram". it will be more better to understand. regards Rathinam.M
|
| Joba | Posted on: 2009/4/25 7:25 |
Developer   Joined: 2006/6/6 From: Posts: 969 |
Re: use of Submachine state ? Hi rathinamsm,
Statemachine state is a syntactical convenience that facilitates reuse and modularity. It is a shorthand that implies a macro-like expansion by another state machine and is semantically equivalent to a composite state. The state machine that is inserted is called the referenced state machine while the state machine that contains the submachine state is called the containing state machine. The same state machine may be referenced more than once in the context of a single containing state machine. In effect, a submachine state represents a “call” to a state machine “subroutine” with one or more entry and exit points. The entry and exit points are specified by stub states. SubmachineState is a child of State. Stub state can appear within a submachine state and represents an actual subvertex contained within the referenced state machine. It can serve as a source or destination of transitions that connect a state vertex in the containing state machine with a subvertex in the referenced state machine. Reference : OMG-Unified Modeling Language, v1.5 2-148 |
| rathinamsm | Posted on: 2009/4/22 16:00 |
Just popping in   Joined: 2009/4/22 From: Posts: 6 |
use of Submachine state ? In State machine diagram.
what is the use of Submachine state and "substate in submachinestate".
|
| Threaded | Oldest First | Previous Topic | Next Topic | Top |